
When students learn to see structure in math, it gives them a new way to think about problem solving.
In Making Sense of Algebra, Paul Goldenberg, June Mark, and their colleagues look carefully at how students think about mathematics. They explore five “Habits of Mind” that focus not just on the results of mathematical thinking, but on how proficient students do that thinking.
In today’s blog, which is the third of five adapted from the book, the authors talk about the habit of seeking and using structure.
Habits of Mind: Seeking and Using Structure
By Paul Goldenberg, June Mark, Jane Kang, Mary Fries, Cynthia Carter, and Tracy Cordner
Building the habit of seeking and using structure begins in the early grades. In elementary school, students meet structure in the notations and naming systems we use, in classification of mathematical objects, and in calculation. They also learn to seek structure by deferring evaluation. Secondary school students see extensions and more complex expressions in algebraic notation, and they encounter and use more complex classifications in both algebra and geometry. They must often decide on an optimal level of evaluation—for example, whether to multiply/factor an expression or leave it as is. And they must often be able to see several alternative structures within an expression and decide which structure best suits the current purpose.
We can develop students’ attention to structure, helping them learn to defer evaluation for certain kinds of tasks. For example, when presented with 7 + 5 ⃝ 7 + 4 and asked to fill in <, =, or > to compare the two expressions, young children are often drawn—and may even be explicitly told—to perform the calculations first. But competent adults, faced with a similar problem “Which is greater, 739 + 43 or 739 + 44?” would never perform the computation first. The competent adult is “strategically lazy” and uses the structure of the calculation, not the results of it, to answer the question.
This is where we want students’ attention: we want them to see the structure rather than focusing on the arithmetic. Without any reference to symbols “standing for” numbers—which is at least distracting and might even be confusing to young learners—they can readily see that it makes no difference what number is behind my hand:
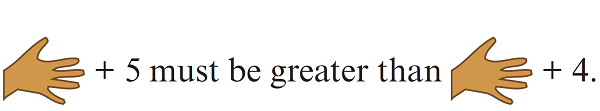
This same habit (and skill) of deferring evaluation—putting off calculation until one sees the overall structure—helps learners notice that they don’t have to find common denominators or do any other “hard” work to compute 1 3/4 – 1/3 + 3 + 1/4 – 2/3. Instead, they see the computation as starting with 3, adding 1 3/4 and 1/4 to that, and then subtracting both 1/3 and 2/3. For any student that could do this “the hard way” on paper, this new approach is a trivial computation that they can do in their heads.
Students need to develop this inclination to look for structure before jumping into calculation so that when they later begin to solve algebraic equations, they are able to use the same idea to treat 3(5x − 4) + 2 = 20 as “something + 2 = 20.”
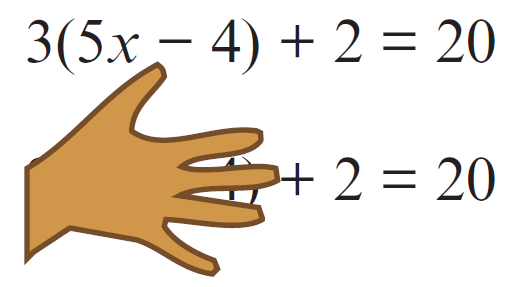
Then, using common sense and not memorized (or mismemorized) rules, the “something” 3(5x − 4) must equal 18. From such reasoning, they can learn to derive rules that make sense. Students in beginning algebra are often taught to solve equations like 2(x + 3) + 4 = 24 by going through a particular set of steps written in a particular way. On successive lines, they might write the original equation, then expand and write a new equation, then combine like terms and write a new equation, then write, on a new line, +10 under both sides, then…, each time writing a new equation. That method works for first-year algebra and helps students “see the steps.” But it doesn’t encourage students to “see beyond the trees” and perceive the overall structure. It’s not that one method is better than the other. Both methods are necessary, because each gives a different insight into the meaning of algebraic expressions and equations. Seeing the structure helps students see the logic of algebra; it often also makes calculation much easier.
♦ ♦ ♦ ♦
 Paul Goldenberg, June Mark, Jane Kang, Mary Fries, and Tracy Cordner work in the Learning and Teaching Division at Education Development Center (EDC), a non-profit organization that designs, implements, and evaluates programs to improve education, health, and economic opportunity worldwide. Cynthia Carter is a mathematics teacher at The Rashi School in Massachusetts.
Paul Goldenberg, June Mark, Jane Kang, Mary Fries, and Tracy Cordner work in the Learning and Teaching Division at Education Development Center (EDC), a non-profit organization that designs, implements, and evaluates programs to improve education, health, and economic opportunity worldwide. Cynthia Carter is a mathematics teacher at The Rashi School in Massachusetts.


