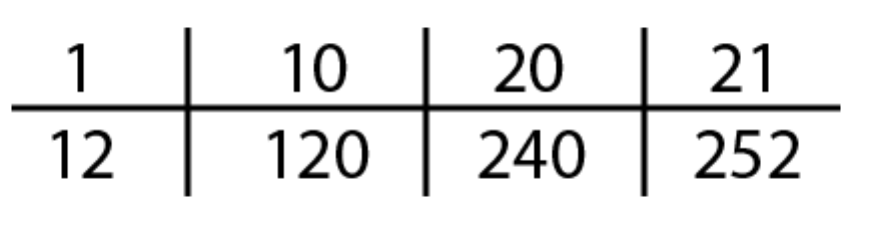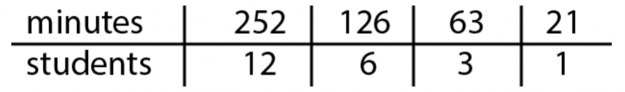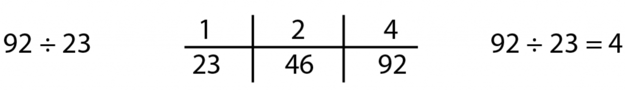by Pam Harris (@pwharris), author of Lessons and Activities for Building Powerful Numeracy
 The second Standard for Mathematical Practice states: “Mathematically proficient students make sense of quantities and their relationships in problem situations. They bring two complementary abilities to bear on problems involving quantitative relationships: the ability to decontextualize—to abstract a given situation and represent it symbolically and manipulate the representing symbols as if they have a life of their own, without necessarily attending to their referents—and the ability to contextualize, to pause as needed during the manipulation process in order to probe into the referents for the symbols involved. Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved; attending to the meaning of quantities, not just how to compute them; and knowing and flexibly using different properties of operations and objects.”
The second Standard for Mathematical Practice states: “Mathematically proficient students make sense of quantities and their relationships in problem situations. They bring two complementary abilities to bear on problems involving quantitative relationships: the ability to decontextualize—to abstract a given situation and represent it symbolically and manipulate the representing symbols as if they have a life of their own, without necessarily attending to their referents—and the ability to contextualize, to pause as needed during the manipulation process in order to probe into the referents for the symbols involved. Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved; attending to the meaning of quantities, not just how to compute them; and knowing and flexibly using different properties of operations and objects.”
If we encourage students to reason quantitatively (attending to the relationships between the numbers and using properties flexibly), they can abstract to general principles that can help solve other seemingly unrelated problems. Here’s one example.
Consider these two different problems:
The first is an example of what is called quotative division. The problem can be thought of as “how many 12’s in 252?” or “12 times what is 252?” That thinking might be recorded as 12 x ____ = 252.
A solution modeled with equations:
12 x 10 = 120
12 x 20 = 240
12 x 1 = 12
12 x 21 = 252
So 252 ÷ 12 = 21
After finding the answer, we need to re-contextualize: 252 minutes divided into 12 minute chunks per students means that the counselor has time to meet with 21 students.
This quotative problem feels multiplicative—you have the total (number of minutes) and the number in each group (how long the meetings are) and you need to find the number of groups (how many students). Many students (and adults!) feel like solving this type of problem using a multiplication strategy.
The second problem is an example of partitive division; it can be thought of as breaking 252 into 12 chunks and finding the size of the chunk. Many beginning students do not feel like this situation is multiplicative at all. Instead they feel like parsing the 252 minutes into 12 chunks (students) and finding out how many minutes are in each chunk. Students might draw 12 circles and deal out tally marks until they have dealt out all of the 252 minutes and then ask how many minutes ended up in each group. This can be tedious and very inefficient.
What if, instead, we encourage students to use the more efficient thinking for problems where it makes sense to do so? We could reason that if it takes 252 minutes for 12 students, then it would take half as long, 126 minutes, for half as many students, 6. It would also take half that time, 63 minutes for half the students, 3. Then 63 minutes parsed by 3 students is 21 minutes per student. This reasoning can be recorded in the following ratio table, with no need to recontextualize because we stayed in context the whole time:
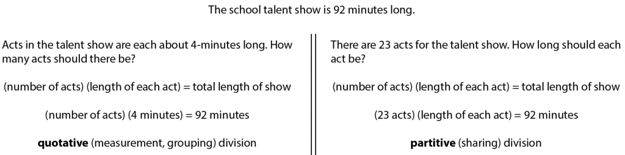
Traditionally, teachers have told students that, since both problems are given as division problems, they should use the same method to solve them: long division. The long division algorithm suggests quotative reasoning. But partitive thinking can be more efficient in some cases.
This time, reasoning about the partitive question as ratios is not particularly helpful, as 92/23 does not simplify to a unit rate easily. Thinking about the problem multiplicatively could look like this:
Or, for the quotative problem, we could find equivalent ratios, reasoning that 92 ¸ 4 = 92/4 = 46/2 = 23. Returning to the context, we reason that 92 minutes divided by 4 minute acts results in 23 acts possible.
The reasoning in this set of problems illustrates what it can mean to “abstract a given situation and represent it symbolically and manipulate the representing symbols as if they have a life of their own, without necessarily attending to their referents.” In this case, reasoning that since each problem represents either 92 ¸ 23 or 92 ¸ 4 respectively, one can solve each problem using the mathematical properties of division.
Students who can use both strategies (dividing by multiplication and by finding equivalent ratios) can then generalize them to other situations. Look what happens with fraction division!
A problem like 5/6 ¸ 1/6 can be thought of quotatively as “how many 1/6’s are there in 5/6?” or 1/6 ´ ____ = 5/6.
How can we as teachers encourage the flexibility and generalized use of strategies discussed above so that students can reason abstractly and quantitatively? One way is to have students solve questions like the school counselor problems, where the numbers are the same even though the situations suggest different thinking. Finding the same solution but using different strategies can cause disequilibrium for students. The teacher can purposefully have students share strategies to solve the different problems and help the students make connections between the solutions. Also teachers can give students problems like those from the talent show, where decontextualizing is helpful because the numbers lend themselves to using properties not suggested by the given contexts.
♦ ♦ ♦ ♦
 Pam Harris is the author of Building Powerful Numeracy for Middle and High School Students, which looks carefully at what research says about developing an instructional approach focused on developing number sense and understanding in higher math. She is also the author of Lessons and Activities for Building Powerful Numeracy, which includes detailed lessons and practical activities that promote strategies for teaching as much mathematics as possible with as little memorization as possible. Follow her on Twitter @pwharris.
Pam Harris is the author of Building Powerful Numeracy for Middle and High School Students, which looks carefully at what research says about developing an instructional approach focused on developing number sense and understanding in higher math. She is also the author of Lessons and Activities for Building Powerful Numeracy, which includes detailed lessons and practical activities that promote strategies for teaching as much mathematics as possible with as little memorization as possible. Follow her on Twitter @pwharris.